Ninguna medición es exacta y nunca se conoce el valor verdadero de la cantidad que se está midiendo.

 

Para remediar los errores aleatorios se pueden tomar repetidas observaciones de la misma medida (observaciones redundantes) y valerse de la ley de probabilidades. Siendo n el número de observaciones y Xi el resultado de cada una de ellas, se puede calcular un valor medio, cercano a la medida exacta:

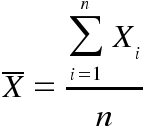
Este valor contiene un error que se expresa en función de la desviación estándar de las observaciones. Para conocer la desviación estándar (sigma) es necesario averiguar la diferencia entre cada observación y la media, lo que se conoce como residuo o error residual (Vi = Xi - Xmedia); de manera que la desviación estándar de la media es:

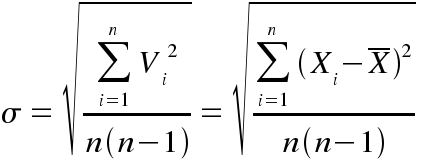
Cuando se realizan varias observaciones los resultados tienden a acumularse al rededor de la media y a distribuirse de una forma particular, denominada curva de distribución normal. Esta curva tiene una típica forma de campana y sirve para determinar un intervalo dentro del que, con determinada probabilidad, se encuentra el valor exacto (o mejor, más probable) de la medición. La amplitud de la curva también permite conocer la precisión de la observación en conjunto.

Las anteriores son curvas de distribución normal en las que el eje de las abscisas marca los intervalos de clase, o el tamaño del residuo escogido para la distribución, y el eje de las ordenadas (el vertical) indica la frecuencia de ocurrencia, o el número de observaciones que caen dentro de cada intervalo. La desviación estándar señala el punto de inflexión de cada curva y, como se dijo antes, la amplitud indica la precisión, de manera que las mediciones que se hicieron para obtener la curva roja fueron más precisas que las de la gráfica azul -nótese que la desviación estándar es menor en el primer caso que en el segundo-. El área bajo la curva indica a su vez la probabilidad de error para un determinado valor. Así que, si se quiere tener una certeza del 50% respecto a una medida, se debe calcular el error probable como:

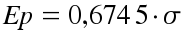
En general, se puede calcular Ep como:

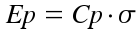
En donde Cp es un factor que sale de una gráfica que relaciona el porcentaje del área bajo la curva de probabilidad y el error. En topografía se utilizan comúnmente los errores del 50%, 90%, 95% (o 2·sigma) y 99,7% (o 3·sigma), los cuales tienen su correspondiente factor:

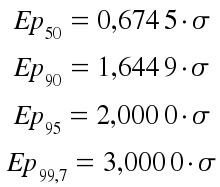
Finalmente se obtiene el valor más probable de la medición como:

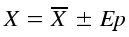
dependiendo de la certeza buscada. El error unitario de la medición se puede calcular con la siguiente expresión:

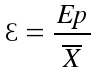
que indica la error que se produjo al medir una unidad, por ejemplo 0,0003 m por cada metro que se mide, y se expresa generalmente como:

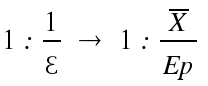
y se lee “uno a ‘inverso del error unitario’” y consiste en el grado de precisión de la medición. También se puede evaluar cada observación por aparte, calculando su desviación estándar:

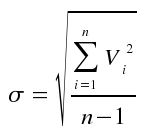
Nótese que la desviación estándar de la observación difiere en una ‘n’ en el denominador del radical, de la desviación estándar de la media. De igual manera, el error probable será:

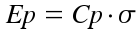
donde Cp es el mismo factor de más arriba y ’sigma’ la desviación estándar de la observación.

Los topógrafos suelen usar el error 3 sigma (Cp = 3) para descartar las observaciones que no caigan dentro de ese rango, pues corresponden a equivocaciones.

Ejemplo

Se mide una misma distancia cinco veces con la misma cinta métrica y en iguales condiciones climáticas obteniendo los siguientes resultados: 19,23 m ; 19,19 m ; 19,27 m ; 19,24 m ; 19,21 m . ¿Cuál fue la distancia medida?

Solución

Hay que tabular los datos de la siguiente manera y aplicar lo explicado en este artículo:

Xi (m)	V (m)	V2 (m2)
19,23	+ 0,002	0,000 004
19,19	- 0,038	0,001 444
19,27	+ 0,042	0,001 764
19,24	+ 0,012	0,000 144
19,21	- 0,018	0,000 324
∑ = 96,14	∑ = 0,000	∑ = 0,003 68

Como el número de mediciones es igual a 5, entonces n=5; por lo tanto, la media es:

Xmedia = 96,14 m / 5 = 19,228 m

La desviación estándar se calcula conociendo la sumatoria de los residuos al cuadrado (0,003 6 y la cantidad de observaciones:

= [(0,003 68)/(5*(5-1))]½ = 0,013 56 m

Aplicando la fórmula para un error probable del 50% (Cp = 0,674 5) se tiene:

Ep = 0,674 5 *(0,01356 m) = 0,009 m

Entonces se puede afirmar que existe un 50% de probabilidad de que la distancia sea:

X = 19,228 m ± 0,009 m

Con estos resultados se puede calcular la precisión con la que se efectuó la medida:

E = 0,009 m / 19,228 m = 0,000 47

Que significa que por cada metro que se midió se cometió un error de 0,000 47 m , que expresado como grado de precisión queda:

Precisión = 1 : 19,228 / 0,009 = 1 : 2 142


lo cual quiere decir que, si se midiera con la misma precisión una distancia de 2 142 m , se cometería un error de 1 m .

Bibliografía

Torres Álvaro y Villate Eduardo. Topografía. Editorial Escuela Colombiana de Ingeniería y Prentice Hall. Bogotá 2001.

Paul Wolf y Russell Brinker. Topografía. Editorial Alfaomega. 2000