Curvas Espirales de Transición

Cuando un vehículo se desplaza por una recta sus ocupantes sólo perciben la sensación de movimiento hacia adelante, producida por la fuerza de impulsión del motor, y, ocasionalmente, la aceleración o deceleración provocada por las maniobras de otros vehículos o por subidas o bajadas en el recorrido. De cualquier manera, el movimiento conserva una única dirección, sin provocar ninguna sensación de inseguridad debido a ello. Sin embargo, cuando el mismo vehículo se adentra en una curva horizontal ocurre un fenómeno generalmente malinterpretado por los estudiosos del diseño de vías.

Para que el vehículo siga la trayectoria curva es necesario que se produzca una aceleración dirigida hacia el centro de la curva. Esta aceleración, denominada aceleración centrípeta (”hacia el centro”, literalmente), es el resultado del giro de los neumáticos del vehículo, que son los que transmiten la fuerza del motor. Es bueno aclarar que no se trata de una fuerza, sino de una aceleración, que también es un vector y que, como ya se dijo va dirigido hacia el centro de la curva, que vamos a suponer que es circular. Lo que sucede es que para los ocupantes del vehículo (que no conforman un cuerpo rígido con él), el cambio de trayectoria es percibido de manera diferente. Si la fricción entre los pantalones (o lo que sea que lleven puesto) y la silla del auto no es suficientemente grande, las personas tienden a seguir su recorrido en línea recta, por inercia diría Newton -de acuerdo a su Primera Ley-, hasta que sean detenidos por alguna parte del vehículo, como la puerta en el caso del conductor; esto es sentido como si existiera una fuerza que quisiera tirarnos hacia afuera de la curva y es lo que muchas personas llaman “fuerza centrífuga” (”hacia afuera del centro”), pero tal fuerza -en un marco de referencia inercial- no existe, es una “fuerza ficticia” y no debe ser incluida en los análisis que conllevan a los caĺculos del diseño geométrico.

Para aclarar un poco el asunto miremos esta gráfica de Newtonian Physics, un libro de física escrito por Benjamin Crowell que se puede descargar libremente (con licencia Creative Commons Share Alike) en el proyecto Ligth and Matter:

1. Cuando se toma como referencia el auto que gira (marco de referencia no inercial), la bola de bolos parece violar las leyes de Newton porque aparentemente se acelera hacia afuera y esa aceleración no es el resultado de una fuerza de interacción con otro objeto.
2. En un marco de referencia inercial, como la superficie de la Tierra, la bola obedece la primera ley de Newton. Ninguna fuerza actúa sobre ella, por lo tanto continua moviéndose en línea recta. Es el vehículo quien está participando en una interacción con el asfalto y se ve sometido a una aceleración (la centrípeta), siguiendo la segunda ley de Newton.

Dejemos la discusión de lado un momento y pasemos a definir dos conceptos que nos van a ayudar más adelante:

Curvatura: Se entiende como el inverso del radio de la curva circular. En recta la curvatura es cero porque el radio se hace infinito, mientras que para una curva de radio Rc se presenta una curvatura igual a 1/Rc. Cuando un vehículo llega a una curva circular simple experimenta una variación repentina de la curvatura, de cero a 1/Rc, en el punto de inicio de la curva (PC), que se mantiene igual a lo largo de toda la curva hasta que termina de nuevo intempestivamente en el PT.

Aceleración centrípeta: La aceleración centrípeta es directamente proporcional al cuadrado de la velocidad del vehículo e inversamente proporcional al radio de la curva, entonces se tiene que $a_c = frac{V^2}{R}$ . Cuando se ingresa en una curva también se presenta un cambio en la aceleración centrípeta, tanto en el PC como en el PT, pasando de una aceleración nula en recta a una definida como $a_c = frac{V^2}{R_c}$ en la curva de radio Rc.

Volviendo a lo que veníamos, tenemos certeza de una cosa: cuando uno conduce el vehículo siente que se va a salir de la curva (especialmente si la velocidad que trae es más alta que la que permite la curva) y reacciona aplicando la dirección hacia adentro de la curva con mayor vigor, provocando que la trayectoria que sigue el auto no describa en realidad una curva circular, causando además una situación potencial de accidente porque invade el carril en el que circulan los vehículos en sentido contrario (en una carretera de dos carriles y dos sentidos). Para remediar esto se han venido utilizando curvas de transición entre la recta y la curva circular que apaciguan la sensación causada por la curvatura y por la aceleración centrípeta.

Estas curvas de transición deben cumplir un objetivo claro: La transición de la curvatura y la de la aceleración centrípeta debe ser constante a lo largo del desarrollo de la curva de transición. Es decir, el radio debe disminuir en una proporción constante a medida que se avanza en la curva, al tiempo que la aceleración centrípeta aumenta.

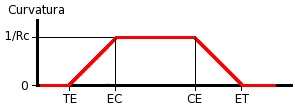
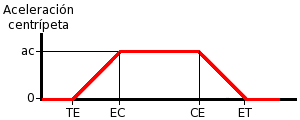
curvatura-con-transicion aceleracion-centripeta-con-espiral

Las anteriores gráficas muestran la transición gradual de la curvatura y la aceleración centrípeta entre el tramo recto (tangente) y la curva circular utilizando una curva de transición, tanto a la entrada como a la salida, como se observa en el esquema de la curva. Los puntos son: TE (Tangente - Espiral), EC (Espiral - Circular), CE (Circular - Espiral) y ET (Espiral - Tangente).

Clotoide o Espiral de Euler

Llamemos $L_e$ a la longitud de la curva de transición y $R_c$ al radio de la curva circular en la que terminará. $a_c$ será la aceleración centrípeta como ya la habíamos definido y $V$ la velocidad de diseño de la vía (se supone que los vehículos circulan a esa velocidad).

Siguiendo el objetivo propuesto para la transición, la variación de la aceleración centrípeta por unidad de longitud está dada por:

$frac{a_c}{L_e} = frac{frac{V^2}{R_c}}{L_e}=frac{V^2}{R_c cdot L_e}$

Para un punto P dentro de la curva de transición, que está a una distancia $L$ desde el comienzo de la curva (punto TE), y al cual le corresponde un radio $R$ , la aceleración centrípeta es:

$a_c = frac{a_c}{L_e}cdot L = frac{V^2}{R_c cdot L_e} cdot L = frac{V^2}{R}$

simplificando $rightarrow R cdot L = R_c cdot L_e$

Pero $R_c$ y $L_e$ son constantes, de manera que su producto se puede denominar $K^2$ , y obtenemos la ecuación de un clotoide, o espiral de Euler, donde K es el parámetro de la espiral:

$R cdot L = K^2$

En esta ecuación R es inversamente proporcional a L, es decir, el radio disminuye de manera proporcional al aumento de la longitud recorrida sobre la curva de transición, que era exactamente lo que se buscaba, pues al disminuir el radio, crece la aceleración centrípeta también en forma gradual.

Elementos geométricos de la espiral

La curva espiral de transición se puede definir en función de los siguientes elementos:

x, y: Coordenadas rectangulares de un punto p (cualquier punto sobre la espiral), referidas a los ejes x e y, donde el eje x coincide con la tangente (la parte recta) y el eje y es perpendicular a ella. El origen de estas coordenadas es el punto TE para la espiral de entrada y el punto ET para la de salida, con dirección positiva hacia el PI -para el eje x- y hacia el centro de la curva (O) -para el eje y-.

θ: Ángulo de deflexión principal para el punto p (De nuevo, el punto p es un punto cualquiera sobre la curva y no debe ser confundido con el punto paramétrico, que es aquel en el que R=L). Éste ángulo se mide entre el alineamiento recto y una recta tangente a la espiral que pase por el punto p.

θe: Ángulo de deflexión principal de la espiral. También es el ángulo que se forma entre una línea perpendicular a la tangente en el punto TE (donde R=∞) y el radio de la curva circular (Rc).

θp: Ángulo paramétrico, es decir, la deflexión principal para el punto en el que R=L.

R: Radio correspondiente al punto p.

Rc: Radio de la curva circular simple que sigue a la espiral.

L: Longitud recorrida sobre la espiral desde el TE hasta el punto p.

dL: Sección infinitesimal de la curva espiral.

dθ: Elemento infinitesimal (diferencial) del ángulo de deflexión principal.

Suponiendo que en una sección infinitesimal la espiral se comporte como un arco circular se tiene (en este caso dθ está en radianes, por ende θ también está en radianes):

$dL = R cdot dthetadtheta=frac{1}{R}dL$

pero $R cdot L =K^2$ , es decir, $frac{1}{R}=frac{L}{K^2}$

entonces $dtheta=frac{L}{K^2}dL rightarrow int{dtheta}=frac{1}{K^2}int{L cdot dL}$

de donde $theta = frac{L^2}{2K^2}$ , o lo que es igual $theta=frac{L^2}{2R_c cdot L_e}$ , o también $theta=frac{L^2}{2R cdot L}=frac{L}{2R}$ . Recordemos que $K^2=R_c cdot L_e = R cdot L$ .

Si queremos encontrar θ en grados sexagesimales, aplicamos los factores de conversión correspondientes:

$theta = frac{90 L^2}{pi cdot R_c cdot L_e}$ y $theta = frac{90 L}{pi cdot R}$ .

Bibliografía

Cárdenas Grisales, James. Diseño Geométrico de Carreteras. Ecoe ediciones. Bogotá. 2002 (Libro disponible en la fotocopiadora de Civil)